| Curves of Stat. Stability | List | Free Surface Effetcs | Trim |
Stability
Displacement
Mass, Weight, Force and Gravity
Mass is the
amount of matter that is contained within a body.
The S.I. units of Mass are:
Grammes
Kilogrammes = 1000 grammes
Metric ton = 1000 kilogrammes
Force is the product of Mass and acceleration
The S.I. Unit of force is:
Kilogramme m/ s2 or Newton (N)
Example: The car hit the tree with a great force. What
would be the great force, this may be calculated by
applying the above.
However the car may not have been speeding or increasing the acceleration but may have been traveling at a constant speed, in that case we come to Momentum
Momentum is
the product of Mass and velocity.
So in case of nautical terms the constant velocity of
a ship is of great importance.
If a ship bangs against a jetty with some velocity
then there will be damage to the jetty but if the same ship reduces her speed
or velocity then the impact damage will be considerably less.
Coming back to Mass and Weight
Weight and Mass are often confused in everyday life.
Weight is actually the resultant force that acts on a
body having some mass.
Weight is thus a product of the mass of the body and
the acceleration due to the earths gravity.
So, the S.I. Units of Weight should actually be kg
m/s2 or Newton (N)
Here since the acceleration due to gravity is known as
9.81m/s2
Therefore we may write:
a mass of 1 kg having a weight of 1kg 9.81 m/s2 as 9.81 kg m/s2
Or simply 1 kgf, which is saying 9.81 N
Or conveniently since 9.81 is constant on the surface
of the earth
We may write the weight to be:
1 kgf, this is the force that is being exerted on a
mass of 1 kg.
But if have to express this in
9.81 N
However again since the gravity factor is common the
unit of Weight is also expressed as kg.
Thus:
1 tonne = 1 metric ton force = 1000 kgf
Or 1 tonne is a measure of 1 metric ton weight.
Moment is the product of force and distance
The S.I. Units of Moment is the Newton-metre (Nm)
Since we have seen that force is expressed in kgf or N
and the S.I. Unit of distance kg is the metre
Thus, 9.81 N = 1 kgf
And, 9810 N = 1000 kgf or 1 tonne
So, the unit generally used for large moments is the tonnes-metre
Pressure is the force that acts on a body to cause it
to change in some form.
If it does not change and there is room for it to move
then it does so.
Pressure is thrust or force per unit area and is
expressed as:
Kilogrammes-force units per square metre or
Kilogrammes-force units per square centimetre or for
larger pressure in tonnes-metre (t/m2)
Density is defined as mass per unit volume or is
expressed as unit of mass per unit of volume
Or grammes/ cubic centimetre
(gms/cc or gms/cm3)
Fresh water has a density of 1 gm/cm3 or
1000kg/m3
Both are correct since:
1 kg is 1000 gms
and 1 metre is 100 cm, since we are talking of cubic quantity 1 cubic metre
would be 100x100x100 cubic cm
So to equate it would be 1000 kg/m3
Or 1 t/m3
Thus the density of FW may be expressed as 1gm/cm3
or 1t/m3
Relative
density is a factor without any unit.
Relative density is expressed as the density of the
substance divided by the density of FW
Thus the RD of FW would be 1/1 or 1
And the RD of SW would be 1.025/1 or 1.025
So basically it is expressed as the same numerical
value but without a unit.
Archimedes found that when a body is immersed in water
then the volume of water that overflowed as a result of this immersion was
equal to the volume of the body.
However the weight of the body plays an important part
in this.
Although the volume of the displaced water is the same
as that of the body the weight may not be the same.
Let us assume that a log of wood of dimension 1metre
by 1metre by 12 metres is taken (thus the volume is 12 metre3, or 12
cbm), let the weight of the log be 8 t. (assumed density of the log at 0.667
t/m3)
This log when it is fully immersed (using external
force) in a tank full of water will make some water overflow, the quantity of
water that would overflow would be 12 metre3, or 12 cbm
But the weight of this water would be 12 t at the
density of 1t/cbm
So we see that the weight of the water is more than
the weight of the fully immersed log of wood and so the log will float.
But at what level?
Now if we remove the force that was holding the log
underwater the log will bounce back to the surface and only a portion of the
log will remain underwater.
This amount will depend on the volume that it
displaces and the weight of that displaced water. Both have to be equal.
If we assume that only 67% of the log is immersed
(12cbm x 0.67) then the volume of the water displaced would also be 8 cbm and
its weight would be 8 t and that was the weight of the log.
So the log would float in a state of equilibrium
However the log would still be capable to taking extra
load, and we can place weight on the log up to a maximum of 4t, any weight
beyond that, and the log would sink.
Let us work out the same example with a bar of iron of
the same dimensions, thus the volume would be 12 cbm and at a density of iron
at 7.86 gm/m3 the weight of the bar would be 94t.
The volume of water that this bar would displace would
be 12 cbm but the weight would be only 12 t.
This being a much lesser figure than the weight of the
iron bar, the iron bar would sink.
Can we now make this bar of iron float?
Yes, we can but we then need to flatten it out to a
sheet of iron.
We then need to bend the four edges so that the sheet
is turned into a open cardboard box.
This will give the iron sheet a much larger volume, the empty space on top of the sheet would also
contribute to the volume but without adding to the weight (assuming the weight
of air to be negligible)
The sheet + air combination however has the same
weight.
Now it will float on the water at a level as
determined by the weight of water that it would displace at that level.
Centre of
Gravity is the point of a body at which all the mass of the body may be assumed
to be concentrated.
The force
of gravity acts vertically downwards from this point with a force equal to the
weight of the body.
Basically
the body would balance around this point.
The Centre
of Gravity of a homogeneous body is at its geometrical centre.
Buoyancy and Centre of Buoyancy
So what makes the log or the open box iron sheet float.
The fact that they are on the surface of the water is
due to the earth’s gravity or the weight of the body.
That it does not sink is due to Archimedes’ principle.
We may also say that a force is pushing up the box.
This force is dependent on the volume of the box within the water as well as
its weight.
This force is termed as the force of Buoyancy.
It will act in case of a uniformly loaded box shaped
vessel through the centre of gravity of the underwater volume of the box.
However if the loading is not uniform, by which we
mean that if say only the fore part is loaded with some other weight then
obviously the underwater volume of the box will change and the centre of
buoyancy will pass through centre of gravity of the new underwater volume of
the box.
Centre of Buoyancy can be defined as the geometrical centre of the underwater volume and
the point through which the total force of buoyancy may be considered to act
vertically upwards with a force equal to the weight of the water displaced by
the body.
Reserve Buoyancy
We have seen the condition of the sheet of iron, which
was turned, into an open cardboard box, which floated very nicely on the
surface of the water.
What happens if you now decide to tilt the box,
depending on how high the edges are the water will enter the enclosed area and
the combination of sheet+ air will become sheet + air + some water.
This may make the box much more heavier
than the weight of the volume of water displaced and the box would sink.
Thus we require to put a
water tight cover on the open box. This would ensure that no water would enter
the open space within the box and the sheet+ air combination would remain
intact and the box would float perpetually.
Thus what we have created is Reserve buoyancy.
A ship in a sea way floats on water, which may be calm
and also may be rough.
When in a rough seaway the ship rides the waves, the
waves support sometimes the ends of the ship and then at the midway mark.
In either of the case the ship would have a tendency
to sink to a lower level since the weight of the ship and that of the water
that it displaces would be different.
Thus the requirement for a
ship to have reserve buoyancy, to meet any eventual sea condition where more
sheet + air combinations would be required to be brought into use.
Coefficient
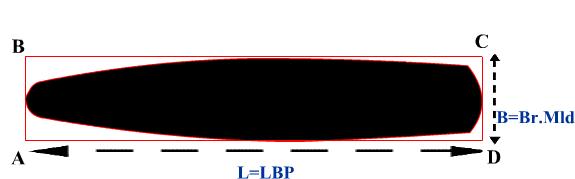
of fineness of water-plane area (Cw):
A ship
floats on water. If at the water line the ship were to be cut off then the area
at the water level is known as the ships water plane
If we now
divide this area of water plane with an imaginary rectangle having the length
similar to the maximum length of the water plane and breadth similar to the
maximum breadth of the water plane then this ration is termed as the
coefficient of fineness of water plane area or Cw
Cw = Area
of water-plane/Area of rectangle ABCD
Similarly
if we know the Cw at a particular draft then we may find the actual water plane
area of the ship by measuring the maximum length and the greatest breadth.
Area of the water-plane = L x B x CW
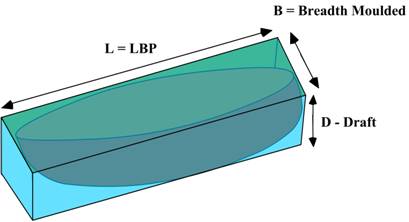
The block
coefficient of fineness of displacement (Cb):
In exactly
the same manner as we obtained the water plane area, if we were to measure the
volume of the underwater part of the ship and divide this with the volume of a
box having its length as that of the ship at that particular draft and breadth
of the box as the maximum breadth of the underwater volume, then we would
arrive at a ratio.
This ratio
is termed as the block coefficient of fineness of displacement,
or Cb
Cb at any
particular draft is the ratio of the volume of displacement at that draft
to the the volume of a rectangular block having the
same overall length, breadth and depth.
Knowing how
the Cb was arrived at, we understand that for a box shaped vessel the ratio of
Cb be 1.
Also finer
the lines of a ship the lower would be the Cb.
Thus a VLCC
would be tending towards 1, whereas a slender yacht or a warship would be
closer to 0.5.
Again this
value of Cb would depend on the draft of that particular ship, since at the
load draft a ship, even a small one appears quite box shaped but as the light
draft is approached the fine curvature of the ship is apparent.
For
merchant ship, this value (depending upon draft) will range from about 0.500 to
0.850, with some typical values as shown below:
ULCC – 0.850 General Cargo ships – 0.700
Oil tankers
– 0.800 Passenger ships – 0.625
Bulk
carriers – 0.750 Container
/ Ro-Ro – 0.575
Tugs
– 0.500
Cb = Volume
of displacement / L x B x draft
Therefore
as in the case of Cw, the underwater volume of a ship may be found at that
particular draft by:
Volume of
displacement = L x B x draft x Cb
The value
of Cb is used to determine the carrying capacity of a Life Boat.
In figure,
the shaded portion represents the volume of the ships displacement at the draft
concerned, enclosed in a rectangular block having the same dimensions.
SHIP’S LIFEBOAT BLOCK COEFFICIENT
The problem
of loading/ declaring the number of persons that it can carry in a Life Boat is
that we do not have any load line marks to guide us.
And even if
there was one it would be difficult to embark looking at the load line mark.
So how is
the number of passengers determined for a life boat.
The block
coefficient of the boat is taken, in this case there is no need to launch the
boat in the water and note the draft.
Say the If
we accept that the Cb of wooden lifeboat is 0.6
Therefore,
volume of the entire lifeboat would be given by
L x B x
draft x 0.6 cubic metres
Now that
the volume of the lifeboat has been found, the next step is to determine the
number of persons that it would safely carry.
To
determine this the following is used and result is the
closest whole number so obtained.
Volume of
the boat / volume of each person
(both in cubic metres)
Here the
size of the person is generally not taken into consideration but the volume is
adjusted with the length of the boat.
For
lifeboat lengths:
7.3 m or
more the volume of a person is taken as 0.283
4.9 m the
volume of a person is taken as 0.396
For
intermediate boat lengths the values
are interpolated.
Effect of
change of density on draft when the displacement is constant
It has been
already explained that the body floats on water at a particular level/ draft,
as long as the weight of the body is equal to the weight of the volume of water
that is displaced by the underwater volume of the body.
Thus the
volume of the water depends on the underwater volume of the body, and
The weight
of this volume of water depends on the density of the water.
Thus when a
ship moves from water of a higher density to a water of lesser density, the
weight of the water volume will become less.
To
compensate for this weight loss an additional volume of water has to be displaced,
this is only possible if the underwater volume of the body is increased.
So the
body/ ship will sink lower in the water of a lesser density, or the draft will
increase.
For box
shaped vessels since the shape is uniform all the way from the top to the
bottom, the walls being all vertical, it is easy to calculate the sinkage or
the rising of the vessel with the change in the density.
The resulting effect on box shaped vessels will be:
New mass of
water displaced = Old mass of water displaced
New volume
x New density = Old volume x Old density
New Volume = Old
density
Old Volume New
density
But volume
= L x B x draft
L x B x New draft = Old density
L x B x Old draft New
density
New draft = Old
density
Old draft New density
The resulting effect on ship shape vessels will be:
New
displacement = Old displacement
New
volume/Old volume = Old density/New density
Due to the
fact that the ships underwater shape is not like a box shaped vessel, the
underwater volume does not linearly change.
To find the
change in draft of a ship shape, the FWA must be known. This is the number of
mm that a ships draft changes when passing from SW to FW.
FWA (in mm)
= Displacement/(4 x TPC).
When the
density of the water lies between these two (SW & FW) then the value (in
mm) that the ships draft changes when she enters the SW is called the Dock
Water Allowance.
DWA (in mm) = FWA (1025 – DW density)/25
Keeping the
draft constant, in effect means that no load has been added or removed.
But if the
draft remains unchanged, even when the density of the water has changed implies
that some change to the displacement has occurred.
Let us
consider:
A ship
floats in the water at a certain draft, therefore the
underwater volume of the ship displaces an equal volume of water. This volume
of water when multiplied with the density of the water gives us the weight of
the water, which again is equal to the weight of the whole ship.
Now if the
density of the water is reduced (travelling from SW to FW), the following would
happen:
The weight
of the displaced water would become less. And consequently to compensate for
this loss in weight an additional volume of water would have to be displaced.
To get an
additional volume of water displaced means that the unde5rwater volume of the
ship has to increase.
If we do
not want the underwater volume of the ship to increase then we have to remove
weights fr0om the ship.
Thus we see
that to keep the draft constant, in a changing density scenario we have to
either lighten the ship or we have add more weights to the ship.
However,
since the draft has not changed, the volume of water displaced also has
remained unchanged.
New vol. of water displaced = Old vol. of water
displaced
New displacement = Old displacement
New density Old
density
New displacement = New density
Old displacement Old
density
Tonnes per
centimetre immersion (TPC)
This is the
mass that must be added/ or removed to a ship in order that the mean draft of a
ship changes by a value of ONE centimetre.
The figures
that are given are for SALT WATER only and corrections have to be applied for
obtaining the values in FW and in other dock waters.
The TPC is
not constant for the ship in all states of loading. The TPC changes as the
underwater form changes, thus the TPC’s are given
against the drafts.
For every
draft there is a different TPC, the most notable changes are between the light
draft and the half way load draft, close to the summer draft the values changes
are very small..
The Tonnes
per Centimetre is therefore dependent on the underwater form of the ship and
this is determined by the water plane at the surface of the water.
So to
calculate the TPC the water plane is essential.
TPC =
(water plane area x density of water) / 100
water plane area (WPA) is in m2
Density is
in t/m3.
Now let the
mass ‘w’ tones be loaded such that the draft increases by 1 cm & the ship
now floats at new Waterline W’L’
Since the
draft increase is by 1 cm the mass loaded is equal to TPC.
Also as the
displaced water quantity increases by some amount, this weight of extra water
displaced equals to TPC as well.
Mass = Volume x Density
= Area x
1/100 x 1.025 tonnes
=
1.025A/100 tonnes
TPCSW = 1.025 A/100
TPCFW = A/100
TPCDW = (RDDW x TPCSW )/1.025
Note: TPC
is always stated for Salt Water unless otherwise specifically mentioned.
Effect of draft and density on TPC
Since the
TPC as has been seen is dependent on the 2 factors:
1. Water
plane area – which determines the underwater volume of the ship
2. And the
density of the water on which the ship is floating
Thus if any of these two factors change the TPC will be affected.
For box
shaped vessels the 1st factor is not applicable since the shape is
uniform all the way from the top to the bottom, the walls are all vertical. The
2nd factor of density needs to be attended to. As the density
increases the TPC also increases.
However for
most ships being ship shaped meaning not box shaped, means that both the
factors affect the TPC. The water plane area would change as the ship sinks
deeper into the water or is lightened. Also the density affects the TPC in the
same way as for a box shaped vessel.
TPC Curves
TPC is
calculated for a range of drafts extending beyond the light and loaded drafts.
This
calculated TPC is then tabulated or plotted in a graphical form and these
graphs are called the TPC curves.
On board a
ship the TPC’s are given in both a tabulated form
alongside the drafts as well as in a graphical form.
Displacement Curves
Displacement
of the ship in SW (1.025) at various drafts is given in both a tabular form as
well as in a graphical form.
A
displacement curve is one from which the displacement of the ship at any
particular draft can be found, and vice versa.
Fresh Water
Allowance (FWA)
In the
basic principle of why a ship floats it is understood that the weight of the
volume of water displaced by a ship is equal to weight of the entire ship.
The volume
of the displaced water is again equal to the volume of the underwater volume of
the ship.
Now when
the weight of this displaced water is calculated we take the product of the
volume of the water and the density of the water.
So, if the
density of the water changes, then the weight of the displaced water changes,
the weight of the ship remaining unchanged.
Thus to
keep the ship floating something has to be adjusted and adjustment is in the
underwater volume of the ship.
So a ship
floating in waters of different densities will do so at different levels.
Thus to
keep the ship floating something has to be adjusted and adjustment is in the
underwater volume of the ship.
So a ship
floating in waters of different densities will do so at different levels.
So we can replace the word level by the nautical word
‘draft’
Thus we may
now define Fresh Water Allowance as the amount in millimetres by which a ships
MEAN DRAFT changes when she moves between SALT WATER and FRESH WATER.
As a ship
moves from SW to FW, the weight of the displaced water reduces – RD of SW at
1.025 and FW at 1.000, so additional volume of water is required to float the
ship, this means that the underwater volume of the ship has to increase so the
ship sinks lower to compensate the above. So the draft increases.
In the same
way if a ship moves from FW to SW, the weight of the displaced water would be
more than the weight of the ship, so the weight of the water has to be reduced,
this may be reduced if the volume of the water is reduced, this again depends
on the underwater volume of the ship, so the underwater volume of the ship is
reduced.
And so the
ship rises a little and the draft of the ship reduces.
FWA (in mm)
= Displacement/ 4x ( (water plane area x density of
water) / 100)
Or FWA =
Displacement / ( 4 x TPC)
Effect of
draft on FWA:
For box
shaped vessel, FWA is the same at all drafts.
For ship
shaped vessels, FWA increases with draft. As the draft increases, both the
displacement and the TPC increase, but the rate of change of displacement is
higher than that of the TPC.
Derivation of the FWA formula
Consider a
ship floating in SW at load Summer draft at waterline
WL.
Let volume
of SW displaced at this draft be ‘V’.
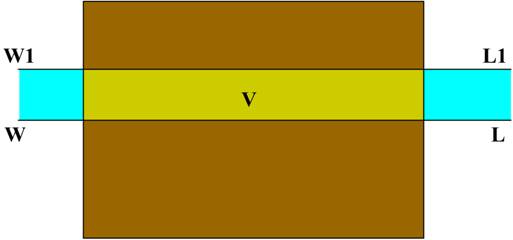
Now let
W1L1 be the waterline for the ship when displacing the same mass of fresh
water.
Let ‘v’ be
the extra volume of water displaced in FW.
Total
volume of fresh water displaced will be V + v.
Mass =
Volume x density
Mass of SW
displaced = 1025V
Mass of
fresh water displaced = 1000 (V + v)
But mass of
FW displaced = Mass of SW displaced.
1000(V + v)
= 1025V
v = V/40
Assume that
‘w’ is the mass of SW in volume v and ‘W’ in volume V,
Then,
replacing the factor
as obtained above we get:
w = W/40
But w is a factor that is a product of the FWA and the
TPC
Now since
the FWA is in mm and the TPC is in cm, they both have to be converted to metres
Thus:
W = (((FWA
mm x 100)cm X TPC cm) / 100 ) metres
Simplifying
we have:
w = (FWA x
100 x TPC) / 100 = W / 40
Or (FWA x
TPC) = W / 40
But w = TPC
x (FWA/10)
Hence W/40
= TPC (FWA/10) or FWA = W/(4 x TPC).
Where ‘W’ =
Loaded SW displacement in tonnes.
Mass =
Volume x density (22*100*12)/100=242=W/40
W=9680
9680/4/12=2420/12=242/1.2=22
Mass of SW
displaced = 1025V
Mass of
fresh water displaced = 1000 (V + v)
But mass of
FW displaced = Mass of SW displaced.
1000(V + v)
= 1025V
v = V/40 TPC = (water plane area x density of
water) / 100
Assume that
‘w’ is the mass of SW in volume v and ‘W’ in volume V,
Then,
replacing the factor
as obtained above we get:
w = W/40
Displacement
= FWA x ( 4 x TPC)
But w = TPC
x (FWA/10)
Hence W/40
= TPC (FWA/10) or FWA = W/(4 x TPC).
Where ‘W’ =
Loaded SW displacement in tonnes.
Dock Water
Allowance (DWA)
As a ship
sails the seas the SW density is assumed to be constant at 1.025 gms/cc, however the density of the SW is never the same
everywhere, especially in partially enclosed salt water bodies, this does not make much difference since the depth of the
water is very substantial.
However
when a ship enters a river from the sea the density of the water changes from
SW to FW, gradually. The density of the river may never attain pure FW
conditions and may be in between.
Thus the need to calculate this intermediate correction for the new
density.
Docks
(enclosed port areas containing jetties) have water that is intermediate
between SW and FW, the water is brackish and may have
a density of 1.010 gms/ cc.
Thus Dock
Water Allowance is similar to FWA and is the amount in millimetres by which the
ships mean draft changes when a vessel moves between a salt water and dock
water.
Dock water is the water whose density is neither that of fresh water or
salt water but in-between the two. RD between 1.000 and 1.025.
To get the
correction in millimetres the formula that may be used is:
(Please
note however that the DWA allowed for should be for the minimum density that
will be encountered by the ship while proceeding to the dock – this as a safety
factor)
DWA = (FWA (1025 – density of dock water)) / 25