| Curves of Stat. Stability | List | Free Surface Effetcs | Trim |
Stability
List
Definitions
Roll: The action of a vessel involving a recurrent motion, usually caused by wave action.
Heel: Semi-permanent angle of inclination caused by
external forces, such as high-speed turns, beam winds, and seas.
List: Permanent angle of inclination, caused by:
1. Ship’s Center of Gravity transversely shifted
from centerline.
2. Negative Metacentric Height (-GM)
3. Combination of Gravity off-centerline and –GM
Moment To Heel 1o Equation
When a ship experiences an Inclining Moment (IM) the
vessel will list or heel until the Righting Moment (RM) is equal to the
Inclining Moment (RM = IM). The Inclining Moment is simply a
force acting through some distance.
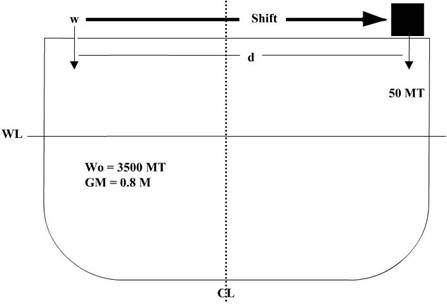
IM = w x d
This is only true when the ship has a negligible
heel or list.
As the vessel inclines, the
distance between the forces changes.
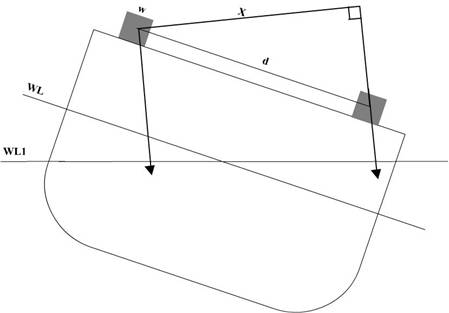
A relationship can be developed to solve for the
distance between forces for all angles of heel. Using an expanded drawing of
the triangle from the above diagram:
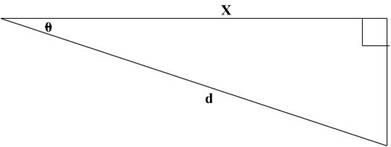
Using the cosine equation to solve for the distance X:
X = d x cos θ
Therefore:
IM = w x d x cos θ
A Righting Moment is created by the ship to keep
itself upright. In this case, the force is equal to the ship’s displacement (WF)
and the distance is the ship’s righting arm (GZ) at each particular angle of
heel.
RM = WF x GZ
The Righting Arm (GZ) changes with inclination of the
ship. Using the relationship derived for small angles of heel:
GZ = GM x sin θ
NOTE: This relationship holds true for angles less
than 7°-10°
Therefore:
RM = GM x WF x sin θ
The initial premise was that RM = IM:
W x d x cos θ = GM x WF x sin θ
Transferring cosine θ to the right:
(sin θ / cos θ) =
tan θ
w x d = GM x WF x tan θ
Choosing a specific angle, the moment (w x d) required
to create that list or heel can be found. Using 1o:
tan 1o
= 0.01746
Therefore:
MH 1˚ = GM x WF x 0.01746
This formula is valid for angles less than 10o
due to movement of the metacenter. To check this
formula for all inclinations less than 10o, a comparison between the
MH10o and 10 times MH1o is made.
MH 10˚ = GM x WF x tan 10˚ -vs- 10 x (MH 1˚ = GM x WF x 0.01746)
MH 10˚ = GM x WF x (0.01746)
And
10 x (MH 1˚) = 10 x GM x WF x (0.01746)
There is a 0.0017 difference over the
10˚range. This error is negligible. The list equation can now be
used.
LIST = (w x d) / MH 1˚
Example
Your ship has a 1.5o list to starboard.
There are 50 MT of cargo placed on the starboard side. The stevedores want to
know how far to transfer the cargo to correct the list.
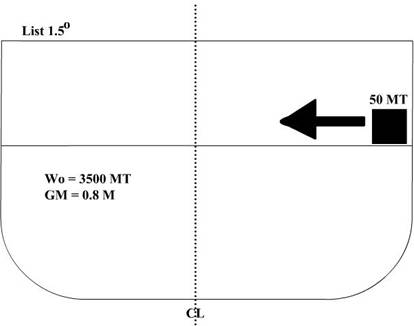
Step 1: Calculate MH1o:
MH 1˚ = GM x WF x (0.01746)
MH 1˚ = 0.8 M x 3500 MT x (0.01746)
MH 1˚ = 48.8 M
Step 2: Use the list equation to solve for distance:
List = (w x d) / MH 1˚
Or, 1.5˚ = (50 MT x d) / 48.8 M
d = (1.5 x 48.8) / 50 = 1.464 M
Example
Your ship has a 2° list to port. The CO wants it
corrected. There are 15 cbm of fuel in the port wing tank (sp.gr.
0.94). The starboard wing tank is empty. Correct the list using the fuel and a
set of 5 cargo pallets (8 MT each). The cargo pallets may only be moved 5 M to
starboard before hitting the bulkhead. How long will it take to correct the
list? Pump capacity is 40 cbm per hour.
WO = 12500 MT
KM = 7.1 M
KG = 6.02 M
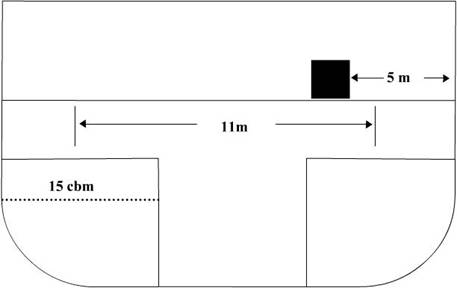
Step 1: Calculate MH1°:
MH 1˚ = GM x WF x (0.01746)
MH 1˚ = (7.1 – 6.02) x 12500 x (0.01746)
MH 1˚ = 235.7
Step 2: Calculate the amount of list corrected by
shifting fuel:
Weight of fuel = 15 x 0.94 = 14.1 MT
List = (w x d) / MH 1˚
Or,
List = (14.1 x 11) / 235.7 = 0.66˚
Step 3: So far, we have corrected 0.66o of
the 2o list. Using the pallets, we will correct for the remaining
1.34o list.
List = (w x d) / MH 1˚ or
d = (1.34 x 235.7) / 40 = 7.9 M
Step 4: Finally, calculate how long it takes to
transfer 15 cbm of fuel when the pump capacity is 40cbm/ hour.
Time = (15 cbm / 40 cbm/h) = 0.375 hr x 60 = 22.5
minutes
Assuming it takes less than 22.5 minutes to move the 5
pallets, this is the time required to correct the list.
Important:
- When attempting
problems on List, first find out the GM of the vessel (if the KG has to be
calculated then do so) if it has not been stated.
- If there are more than
one shifting/ loading/ discharging involved then tabulate the moments and
get the final moment (w x d) to either port or to starboard.
Example:
A ship of 8000 tonnes displacement has KM = 8.7 m, and
KG = 7.6 m. The following weights are then loaded and discharged:
- Load 250 tonnes cargo
KG 6.1m and centre of gravity 7.6m, to starboard of the centre line.
- Load 300 tonnes fuel
oil KG 0.6m, and centre of gravity 6.1m, to port of the centre line.
- Discharge 50 tonnes of
ballast KG 1.2m, and centre of gravity 4.6m, to port of the centre line.
Find the final list.
|
|
Weight |
KG |
Moment about
Keel (V-M) |
|
Orig.
Disp. |
8000 |
7.6 |
60800 |
|
Load |
250 |
6.1 |
1525 |
|
Load |
300 |
0.6 |
180 |
|
Total |
8550 |
|
62505 |
|
Disch. |
-50 |
1.2 |
-60 |
|
Final
Disp. |
8500 |
|
62445 |
Final KG = Final Moment / Final displacement = 62445 / 8500
KG = 7.34
KM = 8.7
Therefore, GM = 1.36
|
w |
d |
Listing
moment |
|
|
|
|
Port |
Stbd |
|
250 |
7.6 |
|
1900 |
|
50 |
4.6 |
|
230 |
|
300 |
6.1 |
1830 |
|
From above we have Port: 1830 and Stbd: 2130
Therefore the final listing moment (w x d) = 300 to
stbd.
Now, MH 1˚ = GM x WF x 0.01746 = 1.36 x 8500 x 0.01746 = 201.8376
List = (w x d) /
MH 1˚ = 300 / 201.8376 = 1.49˚ to stbd.
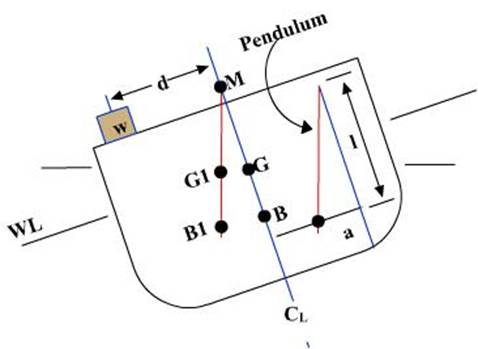
Inclining Experiment
The inclining experiment is completed upon
commissioning of the vessel.
It is performed to obtain accurately the vertical
height of the ship’s center of gravity above the keel (KG).
Procedures:
The shipyard at which the inclining experiment is to
be performed will issue a memorandum to the ship outlining the necessary work
to be done by ship’s force and by the yard to prepare the ship for inclining.
1. Liquid load will be in accordance with the
memorandum.
2. Inventory of all consumables to be made by ship’s
crew and inclining party.
3. Inclining weights are placed on centerline.
4. Freeboard is measured, and a photo of the drafts is
taken.
5. Salinity of saltwater is measured.
8. Pendulums set up forward, midships,
and aft.
9. Weights are moved off-centerline.
10.Inclination of the ship
measured.
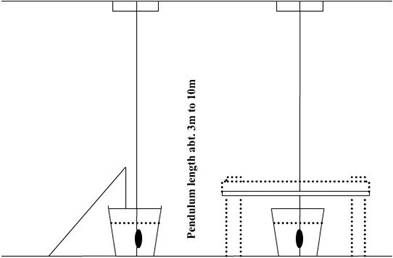
Measurements are taken for several weight movements
both port and starboard. The Naval Architect then uses the following equation:

Where:
w = Inclining Weights (LT)
d = Athwartships Distance Weights Were Moved (FT)
WF = Displacement of Ship (LT, with
Inclining Weights)
tan θ =
Movement of Pendulum ![]() Length
of Pendulum
Length
of Pendulum
The inclining experiment measures GM accurately, and
since the ship’s drafts are known, KM can be found, KG is then found using KG =
KM - GM.