| Curves of Stat. Stability | List | Free Surface Effetcs | Trim |
Stability
Free Surface Effect
Liquid that only partially fills a compartment is said
to have a free surface that tends to remain horizontal (parallel to the
waterline). When the ship is inclined, the liquid flows to the lower side (in
the direction of inclination), increasing the inclining moment.
Background:
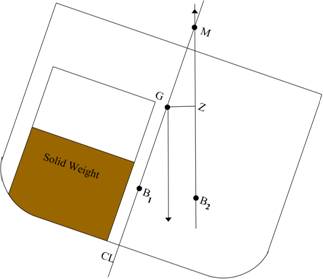
If the tank contains a solid weight, and the ship is
inclined, the center of buoyancy shifts in the direction of the inclination and
righting arms (GZ) are formed.
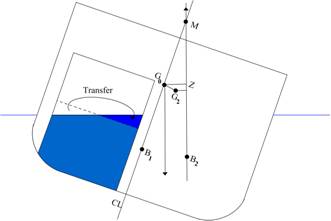
Replacing the solid with a
liquid of the same weight, when the ship is inclined, the surface of the liquid
remains horizontal. This results in a transfer of “a wedge of water,”
which is equivalent to a horizontal shift of weight, causing gravity to shift
from G0 to G2.
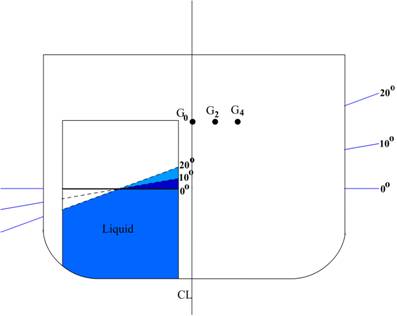
The wedge of water transferred increases as the angle
of inclination increases, therefore, the center of
gravity shifts a different amount for each inclination.
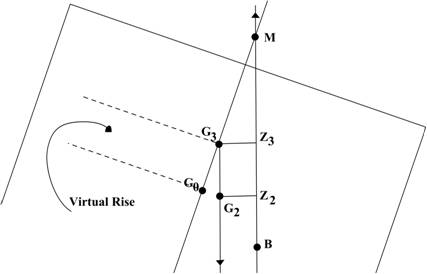
Due to the horizontal shift of the center of gravity,
the righting arm is now G2Z2. To determine the effect on
stability, a vertical line is projected upward through G2 (see
below). Where this line crosses the ship’s centerline is labeled G3.
The righting arm G3Z3 is the same length as the righting
arm G2Z2. Therefore, moving the ship’s center of gravity
to position G2 or G3 yields the same effect on stability.
Movement from G0 to G3 is referred to as a Virtual Rise
of the center gravity.
To calculate the virtual rise in the center of gravity
due to the Free Surface Effect, use the following equation:
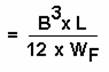
B = The breadth (width) of
the compartment
L = The length of the
compartment
WF = The ship’s
final displacement (after flooding water added)
Factors Effecting Free Surface Effect
Pocketing
Free Surface Effect can be reduced, to some extent, by
creating pocketing. Pocketing occurs when the surface of the liquid contacts
the top or bottom of the tank, reducing the breadth (B) of the free surface
area.
Since the effects of pocketing can not be calculated,
it is an indeterminate safety factor. The Free Surface correction will
therefore indicate less overall stability than actually exists.
Surface
Permeability
Impermeable objects (engines, pumps, piping systems,
etc) inside a flooded space project through and above the liquid surface. These
objects inhibit the moving water and the “shifting of the wedge” may or may not
be complete, thus reducing Free Surface Effect. The impermeable objects also
occupy volume, reducing the amount of flooding water (movable weight) that can
fill the space.
Swash
Bulkheads (Baffle Plates)
In addition to some structural support, these
bulkheads are designed to reduce Free Surface Effect. They are longitudinal
bulkheads that hinder, but do not prevent, the flow of liquid from side to side
as the ship rolls or heels. They are found in tanks, voids, double bottoms,
bilges, etc.
Sluice Valves
Free flow (Sluice) valves on tankers allow opposing
tanks to be cross-connected. When large, partially filled tanks are connected,
Free Surface Effect increases, and the vessel becomes less stable.
Conditions of Free Surface Effect
1. FSE increases with increased length and width of
compartment
2. FSE increases when displacement decreases
(de-ballasting)
3. FSE is independent of the depth of the liquid
Example
Problem
The firemain ruptures,
flooding a compartment with 0.91 metre of saltwater. Displacement prior to
flooding was 4485 MT. The dimensions of the space are: L=9.14m B=12.8m
Calculate the weight added by the flooding water:

2. Calculate the new displacement:

3. Calculate the virtual rise in G due to Free Surface
Effect:
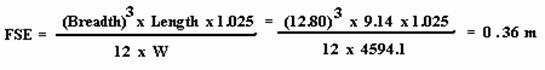
Free Flow Effect
Free Flow Effect occurs when the ship’s hull is
ruptured, allowing sea water to flow in and out as the ship rolls. This
continuous weight addition and removal causes a horizontal shift in the center
of gravity, which then equates to another virtual rise in the center gravity.
Three conditions must exist for Free Flow Effect:
The compartment must be open to the sea.
The compartment must be partially flooded.
The compartment must be off centerline or asymmetrical
about centerline.
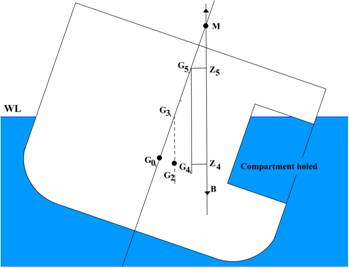
When the vessel below is inclined, it experiences a
horizontal weight shift due to the Free Surface Effect. The center of gravity
shifts from G0 to G2. The center of gravity is shifted
further from centerline due to the flooding weight addition/removal as the ship
rolls. This reduces the righting arm from G2Z2 to G4Z4.
By extending the line of gravitational force up to the centerline, position G5
is found. This increase from G3 to G5 is the virtual rise
of gravity due to the Free Flow Effect.
The virtual rise in the center of gravity due to the
Free Flow Effect (G3G5) is found using the equation:
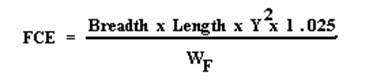
B = Breadth (width) of the compartment
L = Length of the compartment
Y = The distance from the
center of gravity of the compartment to the Centerline of the ship
WF = The ship’s
displacement following damage
The factors which minimize Free Surface Effect
(pocketing, surface permeability, swash bulkheads, etc) will also minimize Free
Flow Effect. There is one additional factor associated with Free Flow: the size
of the hole in the ship.
How the size of the hole affects Free Flow is not
something that can be calculated. The FCE equation does not account for the
hole. Basically, if the hole is small, less water will be added/removed
to/from the ship. The larger the hole, the closer Free Flow Effect is to it’s calculated value.
Example
Problem
A vessel has a hole in the starboard side of a
compartment. Displacement prior to damage was 3700 MT. Flooding depth is 1.52
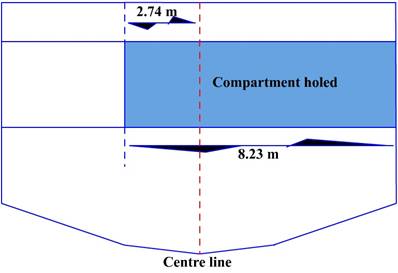
m. Calculate the total virtual rise in the center of gravity (FSE + FCE).
Compartment length is 9.14 and the breadth is 8.23m. The compartment extends
from the Starboard shipside to a distance of 2.74 m beyond the centre line on
the port side.
1. Calculate the weight added due to flooding water:
![]() 2. Calculate the ship’s final displacement:
2. Calculate the ship’s final displacement:
![]()
3. Calculate the virtual rise in G due to Free
Surface Effect:
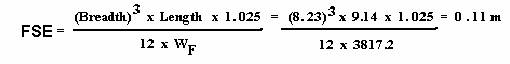
4. Determine the distance “Y” for calculating
the Free Flow Effect:
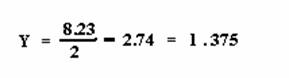
The center of the compartment is 4.11 m from the
inboard bulkhead, and the ship’s centerline is 2.74 m from the inboard
bulkhead.
5. Calculate the virtual rise in G due to Free Flow
Effect:
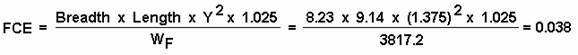
6. Calculate the total virtual rise in the center of
gravity:
GG (virtual) = FSE + FCE = 0.11 + 0.038 =
0.148 m